[Inhalt][0][1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17]
Teil 17 : Suchalgorithmen

Eine Problematik, der man öfters begegnet, ist das der Suche eines vorgegebenen Elements. Auch dabei setzen wir wieder auf die altbewährten Strukturen aus Teil 15. In den Beispielimplementationen benutzen wir Felder und Suchschlüssel (zu findendes Element) des Typs int.
 
simples Suchverfahren

Das wohl erste, was einem Einfällt, wie man ein Suchverfahren realisieren kann ist das Suchen eines Elements, in dem man eine Liste abläuft, bis das gesuchte Element auftritt. Wenn das Element nicht gefunden wurde wird -1 zurückgegeben. Da es bei uns keine negativen Indizes gibt, soll dies unser Fehlercode sein.
 

int SimpelSuchen (int *feld, int Anzahl, int Key)
{
int Index;
for (Index = 0; Index<Anzahl; Index++)
if ( feld[Index] == Key ) return Index;
return -1;
}

Aufgerufen wird das Modul mit dem zu untersuchenden Feld (feld) , der Anzahl der Einträge (Anzahl) und dem zu suchenden Schlüssel (key). Zum Austesten erzeugen wir ein Feld, welches der Einfachheit halber den Indexwert als Feldinhalt besitzt. Außerdem ist es so einfacher zu überprüfen :-)
 

#include <stdio.h> 
#include <stdlib.h> 
#include "struktur.h" 
#include "suchen.h"

#define groesse 10 /* Feldgroesse */ 

void main (void) 
{ 

int *feld = malloc (groesse * sizeof(int)); /* Datenfeld */
int key = 5; /*zu suchender Schlüssel */ 
int Index;

/* Feld belegen, wobei der Inhalt dem Index entspricht */
for (Index = 0; Index<groesse; Index++) feld[Index] = Index;

Index = SimpelSuchen (feld, groesse, key);
if (Index != -1)

printf ("\nAn %dter Stelle ist das Element %d\n\n\n",key,Index);
else
printf ("\n%d nicht gefunden!\n",key);
}

SimpelSuchen Ergebnis bei key=5

Zur Übung könnte man ein dynamisches Feld erzeugen, in dem Daten eingelesen werden und danach nach einem vorgegebenen Schlüssel gesucht wird.
 
 
binäres Suchen

Haben wir ein vorsortiertes Feld vorliegen, so vereinfacht sich die Suche, da wir genau wissen, wo der gesuchte Wert relativ zum aktuellen Feldinhalt liegt. Also ob der Wert kleiner oder größer ist, d.h. rechts- oder linksseitig vom aktuellen Index. Mit anderen Worten, man untersucht die Mitte des zu untersuchenden Feldes, danach die wird die rechte oder linke Teilhälfte das neu zu untersuchende Feld. Bei Fund des Wertes wird der Index zurückgegeben, ansonsten wird solange weitergeteilt, bis rechte und linke Grenze des zu untersuchenden Feldes gleich sind. Dieses Verfahren nennt man binäres Suchen. Ist das Suchen erfolglos geblieben , so gibt es als Rückgabewert -1 , ansonsten den Index des Feldes, in dem sich das gesuchte Element befindet.
 

int binaeresSuchen (int *feld, int Anzahl, int key) 
{ 
int l=0, r=Anzahl-1, mitte;
while( r>=l )
{
mitte = (l+r)/2;
if ( key == feld[mitte] ) return mitte;
if ( key < feld[mitte] ) r = mitte-1;
else l = mitte+1;
}
return -1;
}

Gehen wir den unteren Algorithmus einmal Schritt für Schritt für die Werte eines Feldes der Größe N = 10 und dem Schlüssel key = 7 durch. Wie man sehen kann, arbeitet dieser Algorithmus bei vorsortierten Feldern sehr schnell und hat in unserem Beispiel schon nach 2 Schritten den gesuchten Schlüssel gefunden.
 

 
l
r
mitte
1. Schritt 
0
9
4
2. Schritt 
5
9
7

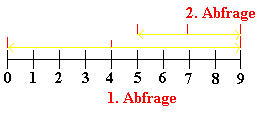
Prinzip des binären Suchen

In der Grafik sind die rechte und linke Grenze, sowie die Mitte rot markiert. Beid der ersten Abfrage umfassen die Grenzen das gesammte Feld. Man weiß man nur, das der gesuchte Schlüssel größer als der Wert im Mittelfeld ist. Daher werden die neuen Grenzen gesetzt und wieder der Wert des Mittelfeldes geprüft. Hier stimmt der gesuchte Wert mit dem Inhalt des geprüften Index überein und dieser wird dann zurückgegeben.
 
suchen in binären Bäumen

In dem Abschnitt über vorsortierte Bäume haben wir das Verfahren kennengelernt, wie man Elemente, die größer als der aktuelle Knoten sind rechtsseitig und kleinere Elemente linksseitig einsortiert.

Beispiel eines vorsortierten Baums

Dieses Verfahren gibt uns wieder eine einfache, aber dennoch schnelle Möglichkeit, Daten zu finden. Dazu vergleichen wir wieder den Schlüssel mit dem aktuellen Element. Ist es größer als unser gesuchter Wert, so suchen wir im linken Ast weiter, ansonsten im rechten Ast. Kommen wir auf ein Feld, das den Wert NULL enthält, so gibt es unseren gesuchten Wert nicht und es wird NULL zurückgegeben. Enthält der aktuelle Knoten das gesuchte Element, so wird der Knoten zurückgegeben. Aufgrund des Aufbaus hängt es sehr stark von der tiefe des Baumes ab, wie schnell ein Element gefunden werden kann.
 

Knoten *BaumDurchsuchen (Knoten *Baum, char key)
{
if (Baum != NULL && Baum->key != key)
{
if (Baum->key > key) return BaumDurchsuchen (Baum->l, key);
else return BaumDurchsuchen (Baum->r, key);
}
return Baum;
}

Erstellen wir ein Beispielprogramm, welches nach einem Schlüssel key sucht. Zusätzlich lassen wir noch nach dem kleinsten und größten Element des Baumes suchen, wie wir es schon im vorigen Kapitel programmierten.
 

#include <stdio.h> 
#include "struktur.h" 
#include "sortier.h" 
#include "suchen.h"

void main (void) 
{ 

Knoten *gesucht = NULL;
Knoten *Baum = NULL; 
char key = 'y';  /* Suchschlüssel */

Baum = SortBaumEinf (Baum, 'b'); 
Baum = SortBaumEinf (Baum, 'x'); 
Baum = SortBaumEinf (Baum, 'd'); 
Baum = SortBaumEinf (Baum, 'a'); 

SortBaumAusgeben (Baum);

if (Baum != NULL)
{

printf("\n\n\nKleinstes Element : %c\n",MinElement(Baum)->key);
printf("\nGroesstes Element : %c\n\n\n\n",MaxElement(Baum)->key);
}
gesucht = BaumDurchsuchen(Baum, key);

if (gesucht != NULL)

printf(">> %c gesucht und %c gefunden\n\n" ,key, gesucht->key);
else
printf(">> %c kommt nicht vor\n\n" ,key);
}

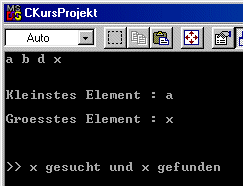
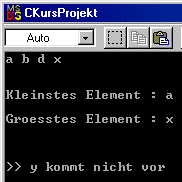
Testen wir mit zwei verschiedenen Schlüsseln, mit einem der existiert und einem, der nicht im Baum enthalten ist, wie das Programm reagiert. Zur Übung kann man auch leere Bäume prüfen lassen und die Sortierroutine ändern , damit Bäume mit Werten vom Typ double untersucht werden.

Element im Baum gefunden

Element nicht gefunden


naives Textsuchen

Ein weiteres Problem, welches in der Praxis recht häufig anzutreffen ist, ist das Suchen eines Textes in einem anderen. Den zu suchende Text nennen wir den Suchtext und den Text, in dem der Suchtext gefunden werden soll Vergleichstext. Das naheliegende naive Verfahren geht dabei den Vergleichstext Buchstaben für Buchstaben entlang und vergleicht ihn mit dem Suchtext, bis er bei Ungleichheit abbricht und den Suchtext eins weiterschiebt. Werden alle Felder vom Suchtext mit dem aktuellen Teil des Vergleichtextes erfolgreich verglichen, so wird der Index, an dem der aktuelle Vergleich startete zurückgegeben.

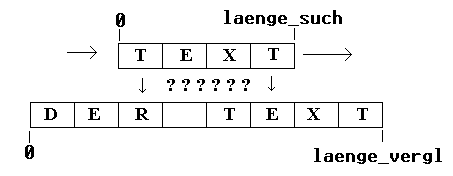
naives Textsuchen

Wenn wir das obere Prinzip verfolgen, so entsteht ein Modul, welches als Parameter den Vergleichs- und den Suchtext benötigt. Um die Funktion strlen ausführen zu können, muß zusätzlich string.h eingebunden sein.
 

#include <string.h>

int  NaiveTextSuche (char *vergleich, char *such)
{

int laenge_such  = strlen(such) ;
int laenge_vergl = strlen(vergleich) ;
int i, j;   /* Laufvariablen */

for ( i=0; i<(laenge_vergl-laenge_such); i++)
{

j=0;
while (vergleich[i+j] == such[j++]) if (j==laenge_such) return i;
}
return -1;
}

Schreiben wir ein Testprogramm, welches einen Suchstring und einen Vergleichstring vorgibt. Die Ausgabe zeigt an, ab welchem Index im Vergleichsfeld der zu suchende String sich befindet.
 

#include <stdio.h> 
#include <stdlib.h> 
#include "struktur.h" 
#include "suchen.h" 

void main (void) 
{ 

int Index;

char *text="Hallo du da, toll nicht ?";
char *such="toll";

Index = NaiveTextSuche( text, such );

if (Index != -1) 

printf("\nAb text[%d] befindet sich im Vergleichstext \"%s\" \n\n",Index,such);
else
printf ("\n%s wurde nicht im Vergleichstext gefunden!\n\n",such);
} 

naive Textsuche Testprogramm

An sich ein kurzes Modul, aber es dauert eben doch seine Zeit, bis er durch lange Texte durch ist. Das wird dann mit dem nächsten Suchverfahren beschleunigt.
 
Knuth-Morris-Pratt Verfahren

Es gibt ein Verfahren, welches sehr effizient Texte durchsuchen kann. Beim naiven Suchen wurde jedesmal, wenn ein Vergleichsfehler auftrat, der Zeiger auf die nächste Textstelle im Vergleichstext nur um 1 erhöht, selbst wenn es im Prinzip unsinnig ist. Um dieses Problem zu umgehen wurde der Knuth-Morris-Pratt Algorithmus von eben jenen namensgebenden Herrschaften entwickelt. Er besteht aus zwei Teilen. Der erste Teil baut eine Sprungtabelle auf, in der aufgelistet ist, um wieviel der Zeiger im Vergleichstext weitergesetzt weren kann, ohne das Gefahr gelaufen wird eine eventuellen Textgleichheit zu versäumen. Diese Tabelle wird auch als Next-Tabelle oder Endstückstabelle bezeichnet. Folgendes Modul baut diese Tabelle auf
 
 

int *KMP_Tabelle( char *Suchtext )
{
int i,j; /* Hilfsvariable */
int suchlaenge = strlen (gesucht);
int *next  = malloc ( suchlaenge * sizeof ( int ));

 /* Speicheranforderung schlug fehl oder kein Feld vorhanden */
 if ((next == NULL) || (feld==NULL)) return NULL;

 next[i=0] = j = -1;

 /* next-Tabelle bilden */
do
{

if (( j<0 ) || ( gesucht[i] == gesucht[j] ))
next[++i] = ++j;
else
j = next[j];
} while ( gesucht[i] );

return next;

}

Aufbauend auf dieser Sprungtabelle sucht nun der Algorithmus das Textfeld ab. Bei jedem nicht übereinstimmen schaut er in der Tabelle nach, um wieviel Buchstaben er im Textfeld weiterspringen kann. Dabei zählt er bei Übereinstimmung, wieviele schon hintereinander richtig stehen. Sind es genausoviele, wie der Suchtext lang ist, so kommt der gesuchte Text im Textfeld vor. Der Algorithmus springt nun raus und übergibt den Index des Textfeldes, ab welchem das gesuchte Wort vorkommt. Am Ende des Textes und der Vergleichsschleife kommt er nur an, wenn keine Übereinstimmung stattfand und er gibt eine Fehlermeldung zurück. Hier nun die Implementierung des Knuth-Morris-Pratt Algorithmus.
 

#include <string.h>

int  KnuthMorrisPratt (char *feld, char *gesucht )
{

 /* Initialisierung der next-Tabelle */

 int i,j; /* Hilfsvariable */
 int suchlaenge = strlen (gesucht);
 int feldlaenge = strlen (feld);
 int *next =  KMP_Tabelle( gesucht ) ; /* Nexttabelle */

 /* Fehler bei der Speicherbelegung */
if (next == NULL ) return -1;

/* Knuth-Morris-Pratt - Algorithmus zur Textsuche*/
 j=0;
 for (i=0; i<feldlaenge; i++)
 {

  /* endlosschleife, die ausgeführt wird
   solange Buchstaben sich überlagern */
  for (;;)
  {
   /* Wenn mindestens 1 Buchstb. übereinstimmt */
   if (feld[i] == gesucht[j])
   {
    j++;
    /* hochzaehlen wieviel Buchstaben schon gleich sind */
    /* bei allen den Index zurückgeben, ab welchem Punkt */
    if (j == suchlaenge) return i-suchlaenge+1;
    break;
   }
   /* keine übereinstimmung, evtl. Sprung ausführen */
   else if (j == 0 ) break;
   else j = next[j];
  }
 }

 /* sind am Ende, keine Übereinstimmung */
 return -1;

}

Zum Abschluß testen wir natürlich noch das Programm
 

#include <stdio.h> 
#include <stdlib.h> 
#include "struktur.h" 
#include "suchen.h" 

void main (void) 
{ 

int Index;

char *text="Hallo du da, toll nicht ?";
char *such="du da";

Index = KnuthMorrisPratt (text, such);

if (Index != -1) 

printf("\nAb text[%d] befindet sich im Vergleichstext \"%s\" \n\n",Index,such);
else
printf ("\n%s wurde nicht im Vergleichstext gefunden!\n\n",such);
} 

KMP-Algorithmus@work


die Datei suchen.h und suchen.c

In den Beispielprogrammen wurde eine Headerdatei suchen.h eingebunden, die alle besprochenen Beispielalgorithmen enthält. Wie das einbinden erfolgt, kann man im Kapitel über den Precompiler nochmals nachlesen.In der Datei suchen.c enthält die Module zu den entsprechenden Datentypen.
 
 

Download suchen.hund suchen.c
suchen.h & suchen.c



 
 
...das Obligatorische

Autor: Sebastian Cyris PCDBascht@aol.com

Dieser C-Kurs dient nur zu Lehrzwecken! Eine Vervielfältigung ist ohne vorherige Absprache mit dem Autor verboten! Die verwendete Software unterliegt der GPL und unterliegt der Software beiliegenden Bestimmungen zu deren Nutzung! Jede weitere Lizenzbestimmung die der benutzten Software beiliegt, ist zu beachten!